一、问题概述
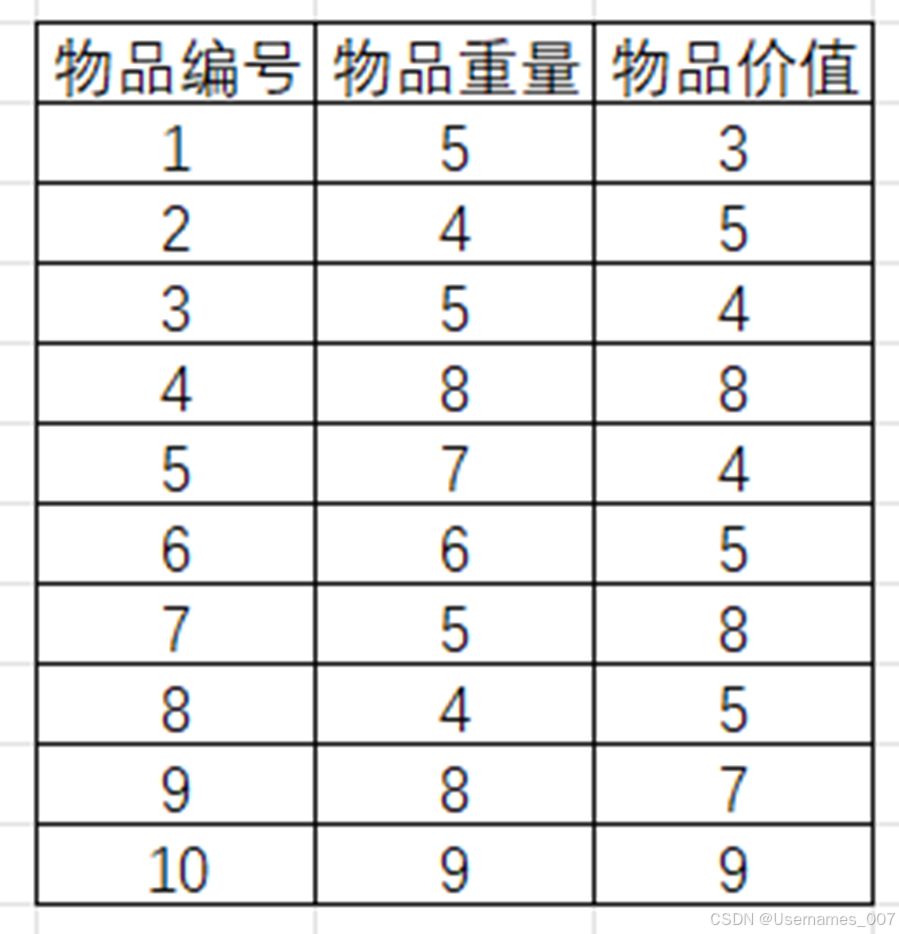
问题概览:给定n种物品和一个背包。物品i的重量是WiWhatsApp网页版,其价值为Vi,背包最大承载重量为C。物品是不可分割的,应如何选择装入背包的物品,使得装入背包中物品的总价值最大。在严格遵循背包最大承载重量C的限制条件下,我们需要挑选决定哪些物品被装入背包中,确保所选择的这些物品的总价值能够达到最大化。
二、回溯算法 1.回溯法概述
回溯法被称为万能解题法,回溯法是一种通过探索所有可能的候选解来找出所有解的算法。如果当前解不满足当前问题,回溯算法会通过在上一步进行一些变化来丢弃该解,即“回溯”,并尝试另一个可能的候选解。回溯法通常用于解决组合优化问题,这些问题可以表示为在解空间树中搜索满足约束条件的解。
在回溯法中,解空间树是表示所有可能解的一个树状结构。树的每个节点代表一个候选解的一部分WhatsApp网页版,树的每个分支代表对候选解的一个扩展。回溯算法从根节点开始,逐步构建候选解,直到达到叶节点之后,检查这个候选解是否满足问题的约束条件。
2.设计思路
使用回溯法来解决0-1背包问题是一种暴力搜索的方法,它尝试所有可能的物品组合,以找到使得背包中物品总价值最大的组合。回溯法通过递归构建解空间树来搜索所有可能的解,并在搜索过程中进行剪枝减少计算量。
3.设计流程
(1)使用递归函数来进行每个物品放入背包或不放入背包的操作。
(2)在每一步递归操作中WhatsApp网页版,都更新当前背包的总重量和总价值。
(3)如果当前背包的总重量超过了最大承载重量C,则回溯,进行剪枝操作,不再计算当前子树下的节点。
(4)到达了递归的终点后,比较当前背包的总价值与之前记录的最大价值,总价值大于记录的最大价值时更新最大值。
4.代码编程
问题的几个变量:

源代码(定义回溯函数为a):
#include
#include
#include
int maxv = 0;
bool selected[10] = {false};
bool selectedPath[10];
void a(int i, int currentWeight, int currentValue, int w[], int v[], int n, int C) {
if (i == n) {
if (currentValue > maxv) {
maxv = currentValue;
memcpy(selected, selectedPath, sizeof(selectedPath));
}
return;
}
a(i + 1, currentWeight, currentValue, w, v, n, C);
if (currentWeight + w[i] <= C) {
selectedPath[i] = true;
int newWeight = currentWeight + w[i];
int newValue = currentValue + v[i];
a(i + 1, newWeight, newValue, w, v, 